Observation
With quality observation
We want to observe the mesh in order to choose an appropriate action to improve mesh regularity.
Nodes scores
The first aspect to consider is the nodes scores.
A node's score is defined as the difference between its ideal adjacency and its actual adjacency:
$$ s_n = d_i - d_a $$
where $s_n$ is the score of vertex $n$, $d_i$ is its ideal adjacency, and $d_a$ is its actual adjacency.
Geometrical quality
We accept only 3 configurations :
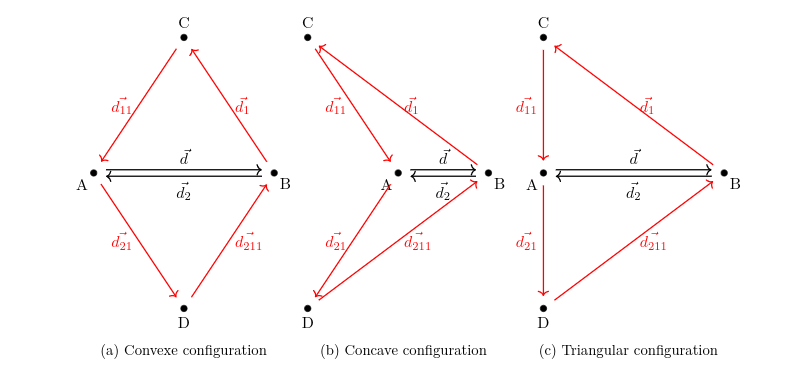
The quadrilaterals shown in Figures (a), (b), and (c) are, respectively, convex, concave, and "triangular". These configurations are distinguished by the orientation of their internal angles and the behavior of their diagonals.
-
A convex quadrilateral is characterized by all internal angles being oriented in the clockwise direction. Equivalently, for each pair of consecutive edges, the signed cross product is strictly negative in a positively oriented coordinate system. In this case, the two diagonals intersect within the interior of the quadrilateral.
-
A concave quadrilateral has exactly one internal angle oriented in the counterclockwise direction. For instance, in figure (b), this can be expressed as:
$$ -\vec{d_{11}} \wedge \vec{d_{21}} > 0 $$
In this configuration, the diagonals do not intersect inside the quadrilateral.
- A "triangular" quadriateral occurs when two adjacent edges are colinear, that is:
$$ -\vec{d_{11}} \wedge \vec{d_{21}} = 0 $$
All other configurations are not supported:
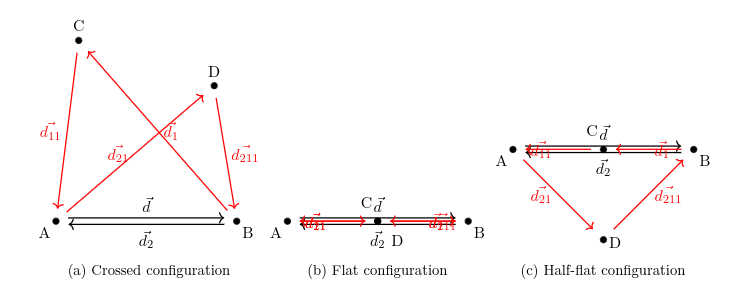
The quadrilaterals shown in Figures (a), (b), and (c) are, respectively, crossed, flat, and "half-flat". These configurations are also distinguished by the orientation of their internal angles and the cross products.
-
A crossed quadrilateral is characterized by two internal angles being oriented in the clockwise direction and two oriented in the other direction. Equivalently, for each pair of consecutive edges, two signed cross product are strictly negative in a positively oriented coordinate system and two are positive.
-
A flat quadrilateral is characterized by all cross products null.
In this configuration, the diagonals do not intersect inside the quadrilateral.
- A half flat quadriateral occurs when two adjacent edges of the same triangular face are colinear, that is:
$$ -\vec{d_{11}} \wedge \vec{d_{21}} = 0 $$
Conclusion
So we charaterized each dart surrounding by its quad associated as :
| Type | boundary | convex | concave | triangular | not defined | not supported |
|---|---|---|---|---|---|---|
| classification id | -1 | 0 | 1 | 2 | -99 | 3,4,5 |